Buying enough Mega Millions tickets to cover every possible combination sounds like a surefire way to win — but there are 3 major problems with that plan
The Mega Millions jackpot is up to $US1.6 billion.
The jackpot is so massive, at least before taxes, that it would theoretically be profitable to buy enough tickets to cover every one of the 302,575,350 possible combinations of Mega Millions numbers.
There are, however, serious logistical problems with such a scheme, and there's a risk of splitting the jackpot and losing money, especially if someone else tries the same thing.
At the time of this writing, the headline Mega Millions jackpot is up to $US1.6 billion, and the lump sum cash grand prize is estimated at $US904 million.
In a Mega Millions drawing, five numbered balls are drawn from a drum with 70 balls, and a final bonus ball is drawn from a drum with 25 balls. If you match all six numbers, you win the full jackpot, and there are smaller fixed prizes awarded for matching some subset of the numbers.
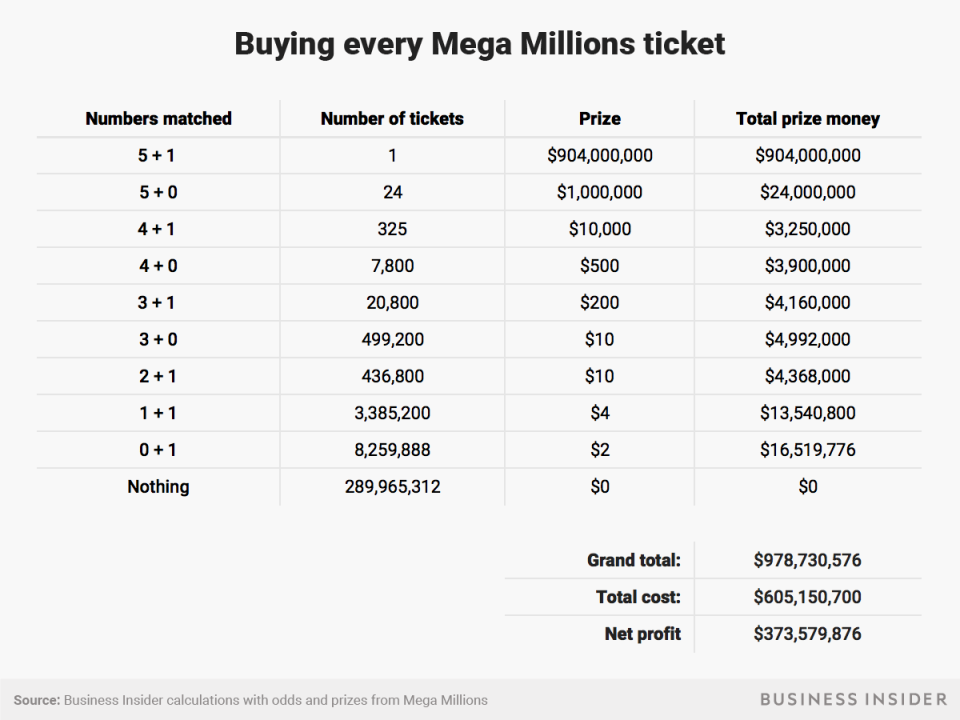
There are 12,103,014 possible combinations of the first five numbers ranging from 1 to 70. Multiply that by the 25 options for the final ball and you get a total of 302,575,350 possible Mega Millions tickets.
At $US2 for each ticket, then, it would be possible to buy every possible ticket for $US605,150,700. As a journalist, I don't have that much money sitting around, but either a consortium of a few million Americans or a large and wealthy institution like a bank could conceivably assemble that level of cash.
With the sky-high jackpot in play, this actually at first glance guarantees a profit - at least before taxes. Since we've bought every ticket exactly once, we can see how much we will win based on the lump sum cash jackpot and the smaller prizes:
Indeed, this is something of a low-ball estimate. As we are buying another half-billion dollars' worth of tickets, part of that money will be added into the jackpot pool.
Of course, there are a few extra complications to this project.
Actually buying 300 million tickets
The first problem is the actual physical act of buying around 300 million Mega Millions tickets and filling them out by hand. Since we need to very carefully and systematically make sure we get every possible ticket, using the computer-generated random quick draw will not work for us.
According to Statista, Wells Fargo has about 232,321 employees. That means that there are about 1,302 possible Mega Millions tickets for each employee. If each employee spent 10 hours a day buying and filling out tickets for three days, this would mean each employee would need to fill out about 43 tickets per hour.
So while this would be extremely difficult to do and perhaps not the best use of a large organisation's resources, it seems that it might be physically possible, if somewhat gruelling, to actually buy every Mega Millions ticket.
Similarly, a large, decentralized consortium of several thousand or a few million Americans connected over the internet - something like an office Mega Millions pool on a mass scale - would be physically capable of buying 300 million lottery tickets.
Of course, the logistical coordination of such a consortium would be a daunting task, and one could imagine various legal and practical difficulties with distributing the money after the drawing.
Splitting the jackpot
The second and larger problem with our comprehensive Mega Millions scheme is the risk of splitting the jackpot. While the fixed prizes do provide about $US75 million of our winnings, the overwhelming bulk of the money comes from the big prize.
That would mean splitting the jackpot two or more ways with other players would be absolutely devastating to our plan. A two-way split cash-prize jackpot would give us $US452 million before taxes. Adding in the fixed prizes, we get a total of about $US527 million in winnings, which is now less than the approximately $US605 million cost of tickets, leaving us a loss of about $US78 million.
The likelihood of splitting the pot is determined by how many other tickets are sold. Business Insider looked at this after the October 19 drawing in which there were no winners, paving the way to the current incredibly high jackpot. Following the logic from that post, we can estimate our odds of winning the jackpot alone based on a few guesses about ticket sales.
According to LottoReport.com, a site that tracks lottery sales and jackpots, 280,217,678 tickets were sold before Friday's drawing. With that many tickets sold, and under the assumption that everyone else playing Mega Millions is picking numbers more or less at random and independently from each other, there's just a 40% chance that we would be the only winner.
We could also expect that, with the $US1.6 billion headline prize, even more tickets will be sold before Tuesday's drawing, greatly hurting our chances of walking away with the full jackpot without having to share.
Other people trying the same thing we are
The above analysis of our odds of splitting the pot assumed that all the other tickets sold were to normal people who would choose their numbers more or less at random. But seeing as we are going all in and buying every ticket, it's possible that someone else could be attempting this as well. There are, after all, several organisations in the US that have the financial and personnel resources to theoretically go out and buy 300 million Mega Millions tickets.
Of course, if two or more banks or consortia tried this plan, they would be certain to have to split the pot and thus lose a bunch of money. This situation is similar to the game Chicken, in which two drivers start out driving directly at each other. If one driver swerves while the other keeps going straight, the first driver "loses" and the second driver "wins." If both drivers swerve, the game is a draw. Naturally, if both drivers keep going straight, their cars crash and they die in a fiery wreck.
In Chicken, the strategy you adopt depends on what you think the other driver is going to do - assuming you're actually playing something as reckless and stupid as Chicken in the first place. If you think he's crazy enough to keep barreling forward, you should be more likely to swerve. If you believe, on the other hand, that he's going to veer out of the way first, then you might be more likely to keep driving straight.
Banks or billionaires with thousands of employees that are considering buying every Mega Millions ticket need to make a similar consideration. If there's a low likelihood that a competitor is going to also mobilize a small army of people in a bid to win a historically high lottery jackpot, then perhaps that risk is worth taking. If, on the other hand, we think that there might be not just one but several other wealthy organisations or people that are making similar plans to our own, we should stay out of the fray.
This used to be much easier
There actually is a precedent for someone buying every ticket in a lottery, thus ensuring that they would be holding a jackpot-winning ticket. Romanian mathematician Stefan Mandel managed to win the lottery 14 times in the 1980s and 90s through a scheme similar to the one considered above.
According to a profile of Mandel in The Hustle, he recruited investors to put up the money needed to buy every ticket in the Virginia lottery. Once the jackpot grew to $US27 million in February 1992 - high enough to make the plan theoretically profitable - Mandel used a bank of computer printers to print out every single combination of numbers from that lottery. A group of couriers then dropped off thousands of tickets at a time at lottery retailers around the state.
Although logistical snags prevented all of the combinations from being entered in time, the consortium still won the $US27 million prize.
However, there are two big reasons why it would be difficult to replicate Mandel's feat. First, the Virginia lottery at the time involved choosing six numbers from 1 to 44. That meant there were 7,059,052 possible tickets in that lottery. While that's a big number and a logistical hassle, it's far lower than the modern multi-state lotteries. Mega Millions' set of 302,575,350 possible tickets is about 43 times larger than the 1992 Virginia lottery.
Second, according to The Hustle, in the wake of Mandel's and similar consortium schemes, state lottery commissions adopted rules banning mass computer-printed lottery tickets. Any attempt to buy every lottery ticket now would require actually filling the tickets out by hand, adding a big hurdle to the strategy.
 Yahoo Finance
Yahoo Finance